Thursday, September 26, 2013 Eric Richards

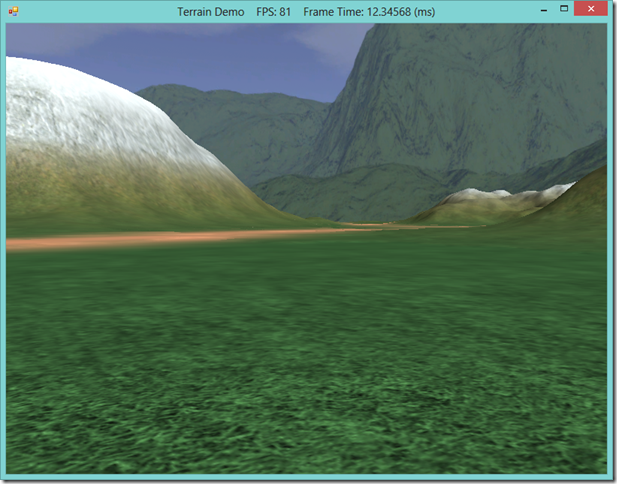
Terrain LOD for DirectX 10 Graphics Cards, using SlimDX and Direct3D 11

Terrain DirectX 11 t-junctions patch-stitching SlimDX C# Tessellation terrain patches

Terrain Patches

In our previous method, we generated a vertex buffer of control points that defined patches of our terrain.  When we drew these terrain patch vertices, our shader code tessellated each patch to generate the final vertices.  Using only DX10-compatible methods, we cannot use the Hull and Domain shaders to perform this tessellation for us, and must instead generate the patch meshes ourselves, on the CPU.  To streamline this process, we will create a new Patch class, which will encapsulate the vertex and index buffers for the mesh representing a terrain patch, and handle creating the patch mesh, rendering the mesh, and all visibility tests for frustum culling the patch.  Our Terrain class will need a list of the patches that make up the landscape, so we will add a List to manage this as a class member variable:

private readonly List<Patch> _patches; 

When we create the terrain, we will need to detect if we can use the DX11 rendering path, or if we will have to fall back to the DX10-compatible render path.  We can query the feature level support of the graphics device in our Init() method in order to determine which rendering method we will need to use.  If we are using a DX11-compatible card, we can create the quad patch buffers as we did previously, but if we are using a DX10-compatible card, we will need to generate the terrain patches using the CPU instead.

We will store which rendering path we will use in the _useTessellation boolean member variable.

public void Init(Device device, DeviceContext dc, InitInfo info) {
    Patch.InitPatchData(CellsPerPatch, device);
    if (device.FeatureLevel == FeatureLevel.Level_11_0) {
        _useTessellation = true;
    }
    // other common setup...
            
    if (_useTessellation) {
        CalcAllPatchBoundsY();
        BuildQuadPatchVB(device);
        BuildQuadPatchIB(device);
    } else {
        BuildPatches(device);
    }
    // more common setup...
}

Building the Terrain Patches

Building the terrain patches for the DX10 rendering method is quite similar to creating the quad patch vertex buffer for the DX11 method.  Our first step is to clear any pre-existing patches, releasing their DX resources if necessary.  Then, we create a terrain patch corresponding to each quad patch, using the grid size defined by our member variables NumPatchVertRows, NumPatchVertCols and CellsPerPatch.  To construct the patch, we will need to define the rectangular bounds of the patch in world-space, so that the patch can construct vertices to match each cell in our heightmap.  After we construct the patch, we add it to our list of patches.

private void BuildPatches(Device device) {
    foreach (var p in _patches) {
        var patch = p;
        Util.ReleaseCom(ref patch);
    }
    _patches.Clear();

    for (var z = 0; z < (NumPatchVertRows - 1); z++) {
        var z1 = z*CellsPerPatch;
        for (var x = 0; x < (NumPatchVertCols - 1); x++) {
            var x1 = x*CellsPerPatch;
            var r = new Rectangle(x1, z1, CellsPerPatch, CellsPerPatch);
            var p = new Patch();
            p.CreateMesh(this, r, device);
            _patches.Add(p);
        }
    }
}

The Patch Class

Each patch will need to maintain a vertex buffer of the points making up the patch, as well as a bounding box that we can use for frustum culling.  We will also cache the source rectangle in the terrain that this patch represents, for debugging purposes.  Since the Patch class is maintaining Direct3D resources, we subclass it from our DisposableClass to ensure that we dispose of those unmanaged resources correctly.

class Patch : DisposableClass {
    public BoundingBox Bounds { get; private set; }
    private bool _disposed;
    private Rectangle _patchBounds;
    private List<TerrainCP> _verts;
    private Buffer _vb;
}

As we will see later, we can re-use the TerrainCP vertex structure that we used earlier for the quad patch control points to represent the vertices of our patch mesh.

When we create the patch mesh, we need to fully tessellate the mesh – that is, we create one vertex for each entry in the height map in the area defined by the patch.  We will assume that the patch bounds rectangle that is passed into our CreateMesh() function is specified in heightmap coordinates, so for each cell of that rectangle, we will create a vertex, converting the heightmap-space rectangle coordinates into the world-space texture position and uv coordinates.  As we create the vertices for the patch, we calculate the minimum and maximum extents of the patch mesh, so that we can create a bounding box for the mesh; because we are using an explicit bounding box here, we can ignore the BoundsY property of the TerrainCP vertex structure, and instead set it to a default value.

public void CreateMesh(Terrain terrain, Rectangle r, Device device) {
            
    _patchBounds = r;
    if (_vb != null) {
        Util.ReleaseCom(ref _vb);
        _vb = null;
    }
            
    var halfWidth = 0.5f * terrain.Width;
    var halfDepth = 0.5f * terrain.Depth;

    var patchWidth = terrain.Width / (terrain.NumPatchVertCols - 1);
    var patchDepth = terrain.Depth / (terrain.NumPatchVertRows - 1);
    var vertWidth = terrain.Info.CellSpacing;
    var vertDepth = terrain.Info.CellSpacing;
    var du = 1.0f / (terrain.NumPatchVertCols - 1) / Terrain.CellsPerPatch;
    var dv = 1.0f / (terrain.NumPatchVertRows - 1) / Terrain.CellsPerPatch;

    _verts = new List<TerrainCP>();
    var min = new Vector3(float.MaxValue);
    var max = new Vector3(float.MinValue);
    for (int z = r.Top, z0 = 0; z <= r.Bottom; z++, z0++) {
        var zp = halfDepth - r.Top / Terrain.CellsPerPatch * patchDepth - z0 * vertDepth;

        for (int x = r.Left, x0 = 0; x <= r.Right; x++, x0++) {
            var xp = -halfWidth + r.Left / Terrain.CellsPerPatch * patchWidth + x0 * vertWidth;
            var pos = new Vector3(xp, terrain.Height(xp, zp), zp);

            min = Vector3.Minimize(min, pos);
            max = Vector3.Maximize(max, pos);

            var uv = new Vector2(r.Left * du + x0 * du, r.Top * dv + z0 * dv);
            var v = new TerrainCP(pos, uv, new Vector2());
            _verts.Add(v);
        }
    }

    Bounds = new BoundingBox(min, max);

    var vbd = new BufferDescription(
        TerrainCP.Stride * _verts.Count,
        ResourceUsage.Immutable,
        BindFlags.VertexBuffer,
        CpuAccessFlags.None,
        ResourceOptionFlags.None,
        0
    );
    _vb = new Buffer(device, new DataStream(_verts.ToArray(), false, false), vbd);
}

Drawing the Patch Meshes

To draw the terrain using the terrain patch list and our DX10 rendering method, we will modify our Terrain.Draw() function.  If we are using the DX11 rendering path, we will use the original rendering code, otherwise, we will use the new DX10-compatible rendering below.  Note that we need to set the DeviceContext’s PrimitiveTopology to render a TriangleList, rather than a PatchListWith4ControlPoints when using DX10.  We will continue to use our TerrainEffect shader effect in this DX10-compatible method, so most of the shader constants that we need to set are the same.  We will need to use a different effect technique, Light1TechNT, which we will define shortly.

We will render our patches by looping over the patch list, rendering only those patches whose bounding boxes pass our camera frustum culling test.

public void Draw(DeviceContext dc, Camera.CameraBase cam, DirectionalLight[] lights) {
    if (_useTessellation) {
        // use previous DX11 rendering code
    } else {
        dc.InputAssembler.PrimitiveTopology = PrimitiveTopology.TriangleList;
        dc.InputAssembler.InputLayout = InputLayouts.TerrainCP;

                
        var viewProj = cam.ViewProj;
        Effects.TerrainFX.SetViewProj(viewProj);
        Effects.TerrainFX.SetEyePosW(cam.Position);
        Effects.TerrainFX.SetDirLights(lights);
        Effects.TerrainFX.SetFogColor(Color.Silver);
        Effects.TerrainFX.SetFogStart(15.0f);
        Effects.TerrainFX.SetFogRange(175.0f);

        Effects.TerrainFX.SetTexelCellSpaceU(1.0f / Info.HeightMapWidth);
        Effects.TerrainFX.SetTexelCellSpaceV(1.0f / Info.HeightMapHeight);
        Effects.TerrainFX.SetWorldCellSpace(Info.CellSpacing);

        Effects.TerrainFX.SetLayerMapArray(_layerMapArraySRV);
        Effects.TerrainFX.SetBlendMap(_blendMapSRV);
        Effects.TerrainFX.SetHeightMap(_heightMapSRV);
        Effects.TerrainFX.SetMaterial(_material);
        var tech = Effects.TerrainFX.Light1TechNT;
        for (var p = 0; p < tech.Description.PassCount; p++) {
            var pass = tech.GetPassByIndex(p);
            pass.Apply(dc);
            for (var i = 0; i < _patches.Count; i++) {
                var patch = _patches[i];
                if (cam.Visible(patch.Bounds)) {
                    patch.Draw(dc, cam.Position);
                }
            }
        }
    }
}

Rendering a Patch

Rendering a patch is relatively straightforward.  At its most basic, we only need to bind the patch’s vertex buffer and an appropriate index buffer to the DeviceContext, then use a DrawIndexed call to render the mesh.  We select the appropriate index buffer by using the Patch’s TessFactor function, which calculates the appropriate LOD level to use based on the distance from the center of the patch’s bounding box to the camera position.

public void Draw(DeviceContext dc, Vector3 camPos) {
    var tessLevel = TessFactor(camPos);
    dc.InputAssembler.SetVertexBuffers(0, new VertexBufferBinding(_vb, TerrainCP.Stride, 0));

    dc.InputAssembler.SetIndexBuffer(IB[tessLevel], Format.R16_UInt, 0);

    dc.DrawIndexed(IndexCount[tessLevel], 0, 0);
}

private int TessFactor(Vector3 eye) {
    var c = (Bounds.Maximum - Bounds.Minimum) / 2 + Bounds.Minimum;
    var d = Vector3.Distance(eye, c);
    var s = MathF.Clamp(-(d - Terrain.MaxDist) / (Terrain.MaxDist - Terrain.MinDist), 0, 1);
    s = 1.0f - s;
            
    return (int)Math.Pow(2, (int)(Terrain.MinTess + (Terrain.MaxTess-1 - Terrain.MinTess) * s));
}

Thus far, we have not discussed the creation of the index buffers for the terrain Patch.  Recall that our vertex buffer contains a vertex for each cell in the fully tessellated terrain patch mesh.  To generate the index buffer for the fully tessellated level-of-detail, we would simply use our standard grid triangulation, as in our GeometryGenerator class.  For our lower levels of detail, we need to combine these triangles into larger triangles.  We will use a power-of-two LOD scheme once again, as it is the easiest to implement.  Where we differ from the previous GPU tessellation scheme is that our LOD scale is inverted; in our GPU shader based code, a tessellation level of 1 meant that we generated one quad per patch, whereas here, a tessellation level of 1 means that we generate the fully tessellated mesh.  This is why the TessFactor() function differs from the HLSL CalcTessFactor() function on which it is based.

private static void BuildIndices(Device device) {
    for (var tessLevel = 0; tessLevel <= 6; tessLevel++) {
        var t = (int)Math.Pow(2, tessLevel);
        var indices = new List<short>();
        for (int z = 0 , z0 = t; z < width; z += t, z0 += t) {
            for (int x = 0, x0 = t; x < width; x += t, x0 += t) {
                indices.Add((short)(z0 * (width + 1) + x0));
                indices.Add((short)(z0 * (width + 1) + x0 + t));
                indices.Add((short)((z0 + t) * (width + 1) + x0));

                indices.Add((short)((z0 + t) * (width + 1) + x0));
                indices.Add((short)(z0 * (width + 1) + x0 + t));
                indices.Add((short)((z0 + t) * (width + 1) + x0 + t));
            }
        }

        var ibd = new BufferDescription(
            sizeof(short) * indices.Count,
            ResourceUsage.Dynamic,
            BindFlags.IndexBuffer,
            CpuAccessFlags.Write,
            ResourceOptionFlags.None,
            0
            );

        if (IB != null) {
            if (indices.Count > 0) {
                IB[t] = new Buffer(
                    device, 
                    new DataStream(indices.ToArray(), false, true), 
                    ibd
                );
            } else {
                IB[t] = null;
            }
        }
       IndexCount[t] = indices.Count;
    }
}

Using this technique, we have created an appropriate set of index buffer to render the terrain patches at various levels of detail.  If you run this code, however, you will see that this technique is not perfect.  Sometimes, at the joints between patches of different LODs, you will notice gaps in the mesh appearing.  These gaps are known as T-Junctions, and are caused by the extra vertices in the higher-detail mesh creating edges which do not match up with the edges in the lower-detail mesh.

There are many solutions to fixing up t-junctions.  The method shown here is relatively simple, and give fairly decent results.  We will split up each patch into three portions: the top edge, the left edge, and the interior.  The interior portion of the mesh (which includes the right and bottom edges), will always use the same index buffer for a given patch tessellation level.  The top and left portions will use one of three index buffers, depending on the tessellation level of the adjacent patch:

• The patches have the same level of tessellation – In this case, we will tessellate the edge portion the same as the interiors.
• The neighboring patch is more detailed than this patch – In this case, we will need to stitch the higher-detail triangles of the adjacent patch to the lower-detail triangles of this patch.
• The neighboring patch is less detailed than this patch – In this case, we need to stitch the lower-detail triangles up to this patch’s high-detail triangles.

We can take advantage of the fact that the most any two adjacent patches will differ in detail level is one level, according to our LOD formula.  This cuts down on the number of combinations that we need to compute considerably.

The interior index buffers are the simplest to compute, since the algorithm is very similar to the method used above to compute the index buffer for the entire patch.  We need to create one index buffer for each of our detail levels.  The index buffer generated will describe a triangle mesh that is one quad smaller in each dimension than the entire patch, where the omitted quads are for the left and top edges of the patch.  We will store the generated index buffers in a dictionary where the key is the tessellation level of the patch, and the value is the index buffer at that tessellation level.  We will also need to store the number of indices in each index buffer in a similar dictionary.

private static readonly Dictionary<int, Buffer> CenterIB = new Dictionary<int, Buffer>();
private static readonly Dictionary<int, int> CenterIndexCount = new Dictionary<int, int>();

private static void BuildCenterIndices(Device device) {
    for (var tessLevel = 0; tessLevel <= 6; tessLevel++) {
        var t = (int)Math.Pow(2, tessLevel);
        var indices = new List<short>();
        for (int z = 0 + t, z0 = t; z < width; z += t, z0 += t) {
            for (int x = 0 + t, x0 = t; x < width; x += t, x0 += t) {
                indices.Add((short)(z0 * (width + 1) + x0));
                indices.Add((short)(z0 * (width + 1) + x0 + t));
                indices.Add((short)((z0 + t) * (width + 1) + x0));

                indices.Add((short)((z0 + t) * (width + 1) + x0));
                indices.Add((short)(z0 * (width + 1) + x0 + t));
                indices.Add((short)((z0 + t) * (width + 1) + x0 + t));
            }
        }

        var ibd = new BufferDescription(
            sizeof(short) * indices.Count,
            ResourceUsage.Dynamic,
            BindFlags.IndexBuffer,
            CpuAccessFlags.Write,
            ResourceOptionFlags.None,
            0
            );

        if (CenterIB != null) {
            if (indices.Count > 0) {
                CenterIB[t] = new Buffer(
                    device, 
                    new DataStream(indices.ToArray(), false, true), 
                    ibd
                );
            } else {
                CenterIB[t] = null;
            }
        }
        CenterIndexCount[t] = indices.Count;
    }
}

Generating the edge index buffers is more complicated, since we need to cover three cases.  Calculating the top and left edges follows the same pattern, so we will only present the method for the left edges here.  We will store these index buffers in another set of dictionaries, keyed by the direction to the adjacent patch, either Left or Top.  The values of the index dictionary will be another dictionary, which will be keyed by a Tuple, which will contain the patch tessellation level and its neighbor’s tessellation level, with the value being the index buffer for that transition.  We will again maintain a parallel dictionary storing the number of indices in each index buffer.

internal enum NeighborDir {
    Top, Left
}

private static readonly Dictionary<NeighborDir, Dictionary<Tuple<int, int>, Buffer>> EdgeIbs = 
    new Dictionary<NeighborDir, Dictionary<Tuple<int, int>, Buffer>>();
private static readonly Dictionary<NeighborDir, Dictionary<Tuple<int, int>, int>> EdgeIndiceCount = 
    new Dictionary<NeighborDir, Dictionary<Tuple<int, int>, int>>();

Constructing the edge index buffer between two patches of equal level-of-detail is relatively straightforward, since we can follow the same triangulation pattern as above.

private static void BuildLeftEdges(Device device) {
    BufferDescription ibd;
    EdgeIbs[NeighborDir.Left] = new Dictionary<Tuple<int, int>, Buffer>();
    EdgeIndiceCount[NeighborDir.Left] = new Dictionary<Tuple<int, int>, int>();

    Tuple<int, int> key;
    List<short> indices;
    int x0;
    int t;
    for (int i = 0; i < 6; i++) {
        t = (int)Math.Pow(2, i);
        key = new Tuple<int, int>(t, t);
        indices = new List<short>();
        x0 = 0;
        for (int z = 0, z0 = 0; z < width; z += t, z0 += t) {
            indices.Add((short)(z0 * (width + 1) + x0));
            indices.Add((short)(z0 * (width + 1) + x0 + t));
            indices.Add((short)((z0 + t) * (width + 1) + x0));

            indices.Add((short)((z0 + t) * (width + 1) + x0));
            indices.Add((short)(z0 * (width + 1) + x0 + t));
            indices.Add((short)((z0 + t) * (width + 1) + x0 + t));
        }

        ibd = new BufferDescription(
            sizeof(short) * indices.Count,
            ResourceUsage.Dynamic,
            BindFlags.IndexBuffer,
            CpuAccessFlags.Write,
            ResourceOptionFlags.None,
            0
            );
        EdgeIbs[NeighborDir.Left][key] = new Buffer(device, new DataStream(indices.ToArray(), false, false), ibd);
        EdgeIndiceCount[NeighborDir.Left][key] = indices.Count;
    }

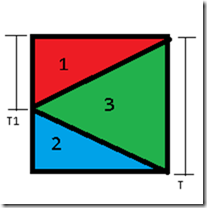
Constructing the edge between a patch and a patch of greater detail is the next simplest.  For each quad cell in this patch, we need to build three edge triangles, shown in the diagram below.  Here, T is the grid size of the current patch, while T1 is the grid size of the higher-detail patch.  We can take advantage of the observation that, if this patch is at detail level T, then the neighboring patch on the top will also be at level of detail T, or level of detail T+N, due to the way in which we are calculating level-of-detail levels according to distance, so we do not need to worry about any issues stitching this patch to a higher level of detail patch on the top.

for (var i = 1; i <= 6; i++) {
    t = (int)Math.Pow(2, i);
    var t1 = (int)Math.Pow(2, i - 1);
    key = new Tuple<int, int>(t, t1);
    indices = new List<short>();
    x0 = 0;

    for (int z = 0 , z0 = 0; z < width - t1; z += t, z0 += t) {
        indices.Add((short)(z0 * (width + 1) + x0));
        indices.Add((short)((z0) * (width + 1) + x0 + t));
        indices.Add((short)((z0 + t1) * (width + 1) + x0));

        indices.Add((short)((z0 + t1) * (width + 1) + x0));
        indices.Add((short)((z0 + t) * (width + 1) + x0 + t));
        indices.Add((short)((z0 + t) * (width + 1) + x0));

        indices.Add((short)((z0) * (width + 1) + x0 + t));
        indices.Add((short)((z0 + t) * (width + 1) + x0 + t));
        indices.Add((short)((z0 + t1) * (width + 1) + x0));
    }

    ibd = new BufferDescription(
        sizeof(short) * indices.Count,
        ResourceUsage.Dynamic,
        BindFlags.IndexBuffer,
        CpuAccessFlags.Write,
        ResourceOptionFlags.None,
        0
        );
    EdgeIbs[NeighborDir.Left][key] = new Buffer(device, new DataStream(indices.ToArray(), false, false), ibd);
    EdgeIndiceCount[NeighborDir.Left][key] = indices.Count;
}

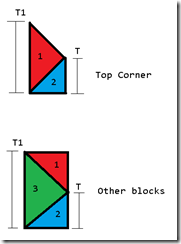
Constructing the edge when this patch is at a lesser level of detail than the neighboring patch is more complicated, since we need to handle the top corner of the edge differently than the rest of the edge.  In this case, the patch above the current patch will be at a greater tessellation level than the current patch as well as the left patch, so we need to be careful that we construct the index buffer to stitch to that corner as well.  You can see how these triangles are setup in the diagram below:

for (var i = 0; i < 6; i++) {
    t = (int)Math.Pow(2, i);
    var t1 = (int)Math.Pow(2, i + 1);
    key = new Tuple<int, int>(t, t1);
    indices = new List<short>();
    x0 = 0;

    indices.Add(0);
    indices.Add((short)((width+1) + t));
    indices.Add((short)(t1*(width+1)));

    indices.Add((short)((width + 1) + t));
    indices.Add((short)(t1 * (width + 1) + t));
    indices.Add((short)(t1 * (width + 1)));

                
    for (int z = 0+t1, z0 = t1; z < width; z += t1, z0 += t1) {
        indices.Add((short)(z0 * (width + 1) + x0));
        indices.Add((short)(z0 * (width + 1) + x0 + t));
        indices.Add((short)((z0 + t) * (width + 1) + x0 + t));

        indices.Add((short)((z0 + t) * (width + 1) + x0 + t));
        indices.Add((short)((z0 + t1) * (width + 1) + x0 + t));
        indices.Add((short)((z0 + t1) * (width + 1) + x0));

        indices.Add((short)(z0 * (width + 1) + x0));
        indices.Add((short)((z0 + t) * (width + 1) + x0 + t));
        indices.Add((short)((z0 + t1) * (width + 1) + x0));
    }
                
    ibd = new BufferDescription(
        sizeof(short) * indices.Count,
        ResourceUsage.Dynamic,
        BindFlags.IndexBuffer,
        CpuAccessFlags.Write,
        ResourceOptionFlags.None,
        0
        );
    EdgeIbs[NeighborDir.Left][key] = new Buffer(
        device, new DataStream(indices.ToArray(), false, false), ibd);
    EdgeIndiceCount[NeighborDir.Left][key] = indices.Count;
}

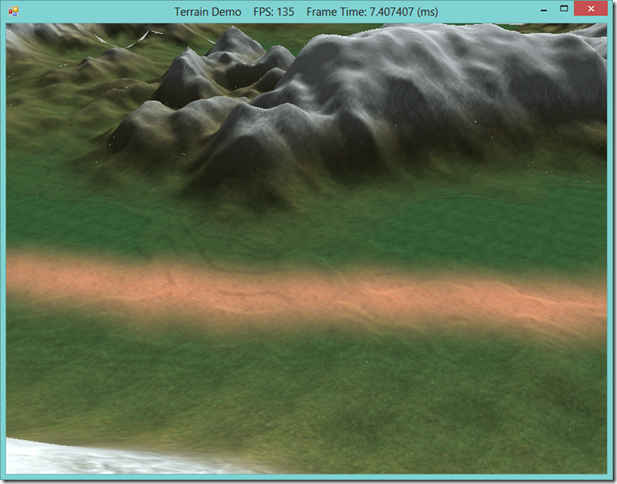
In the screenshot below, you can see the edge transitions using patch stitching.

Rendering the patches with Edge Stitching

To correctly render the patches with the edge stitching technique just presented, we need to have access to the neighboring patches on the top and left of each patch that we render.  We will modify our Draw() function in our Terrain class to support this.  We will construct a dictionary indexed by the neighboring patch direction, containing the neighbors of this patch.  If the patch is on the top or left edge of the terrain, then we will need to add a null neighbor for the patch.

for (var p = 0; p < tech.Description.PassCount; p++) {
    var pass = tech.GetPassByIndex(p);
    pass.Apply(dc);
    for (var i = 0; i < _patches.Count; i++) {
        var patch = _patches[i];
        if (cam.Visible(patch.Bounds)) {
            var ns = new Dictionary<NeighborDir, Patch>();
            if (i < NumPatchVertCols) {
                ns[NeighborDir.Top] = null;
            } else {
                ns[NeighborDir.Top] = _patches[i - NumPatchVertCols+1];
            }
            if (i % (NumPatchVertCols-1) == 0) {
                ns[NeighborDir.Left] = null;
            } else {
                ns[NeighborDir.Left] = _patches[i - 1];
            }
            patch.Draw(dc, cam.Position, ns);
        }
    }
}

To render the patch, we will modify the Patch class Draw() function to accept the patch neighbor dictionary we have just created as a parameter. First, we will render the patch interior, according to the calculated level-of-detail value of the current patch. Next, we need to calculate the level-of-detail values for the top and left neighbors. If the neighbor is null, we will instead use the level-of-detail value of this patch to draw the edge.  Once we have calculated the level-of-detail value of the neighboring patch, we construct the tuple that we will use to index into our edge index buffer dictionaries for the neighbor’s direction, where the first element is the level-of-detail of this patch, and the second element is the level-of-detail value of the neighboring patch.  Once we have constructed this tuple key, we can select the correct index buffer from our dictionary to use when rendering the edge mesh.

public void Draw(DeviceContext dc, Vector3 camPos, Dictionary<NeighborDir, Patch> neighbors) {
    var tessLevel = TessFactor(camPos);
    dc.InputAssembler.SetVertexBuffers(0, new VertexBufferBinding(_vb, TerrainCP.Stride, 0));

    dc.InputAssembler.SetIndexBuffer(CenterIB[tessLevel], Format.R16_UInt, 0);

    dc.DrawIndexed(CenterIndexCount[tessLevel], 0, 0);

    int topEdge = neighbors[NeighborDir.Top] != null ? neighbors[NeighborDir.Top].TessFactor(camPos) : tessLevel;
    var key = new Tuple<int, int>(tessLevel, topEdge);
    if (EdgeIbs[NeighborDir.Top].ContainsKey(key)) {
        dc.InputAssembler.SetIndexBuffer(EdgeIbs[NeighborDir.Top][key], Format.R16_UInt, 0);
        dc.DrawIndexed(EdgeIndiceCount[NeighborDir.Top][key], 0, 0);
    }
    int leftEdge = neighbors[NeighborDir.Left] != null ? neighbors[NeighborDir.Left].TessFactor(camPos) : tessLevel;
    key = new Tuple<int, int>(tessLevel, leftEdge);
    if (EdgeIbs[NeighborDir.Left].ContainsKey(key)) {
        dc.InputAssembler.SetIndexBuffer(EdgeIbs[NeighborDir.Left][key], Format.R16_UInt, 0);
        dc.DrawIndexed(EdgeIndiceCount[NeighborDir.Left][key], 0, 0);
    }

}

Optimizing the Index Buffers

You may have noticed that we declared all of these index buffer dictionaries as static.  This means that there will only be a single copy of these index buffers for all of our Patch instances.  Assuming that the dimensions of all of our patches are the same, these index buffers will always be the same for all our patches, so we can save a tidy amount of memory and processing cycles by only calculating and storing these buffers once.  We will add a public static function to cache the patch size and generate these index buffers.  This function needs to be called once prior to drawing the patches; we will do this at the beginning of our Terrain.Init() function.

public static void InitPatchData(int patchWidth, Device device) {
    width = patchWidth;
    BuildCenterIndices(device);
    BuildTopEdges(device);
    BuildLeftEdges(device);
}

The Result

As you can see, we have eliminated most of the T-junctions present in the terrain mesh using this technique.  You may still see some small gaps, so it is highly possible that this algorithm is not perfect, however, I have not noticed any glaring issues.  Using an appropriate skybox that matches the general color scheme of you terrain textures can mitigate any remaining t-junction issues for the most part.

Additions to the Terrain.fx Shader File

We will need to add some additional techniques to our shader effect for our non-GPU tessellated rendering path.  We can reuse our current terrain pixel shader, but we will need to create a new vertex shader that combines the operations of our previous vertex and domain shaders, in order to generate a DomainOut vertex structure that we can pass into the pixel shader.  This means that we will have to generate the tiled texture coordinate that the pixel shader uses to map the diffuse textures, set the height of the vertex position by sampling the heightmap texture, and project the vertex’s world position into homogeneous screen space.  The new vertex shader and the new effect technique definitions follows:

DomainOut VS_NT(VertexIn vin)
{
    DomainOut vout = (DomainOut)0;
    
    // Terrain specified directly in world space.
    vout.PosW = vin.PosL;
    // Output vertex attributes to next stage.
    vout.Tex      = vin.Tex;
    vout.TiledTex = vout.Tex * gTexScale;
    vout.PosW.y = gHeightMap.SampleLevel( samHeightmap, vout.Tex, 0 ).r;
    vout.PosH    = mul(float4(vout.PosW, 1.0f), gViewProj);
        
    return vout;
}

technique11 Light1NT
{
    pass P0
    {
        SetVertexShader( CompileShader( vs_4_0, VS_NT() ) );
        SetGeometryShader( NULL );
        SetPixelShader( CompileShader( ps_4_0, PS(1, false) ) );
    }
}
technique11 Light2NT
{
    pass P0
    {
        SetVertexShader( CompileShader( vs_4_0, VS_NT() ) );
        SetGeometryShader( NULL );
        SetPixelShader( CompileShader( ps_4_0, PS(2, false) ) );
    }
}
technique11 Light3NT
{
    pass P0
    {
        SetVertexShader( CompileShader( vs_4_0, VS_NT() ) );
        SetGeometryShader( NULL );
        SetPixelShader( CompileShader( ps_4_0, PS(3, false) ) );
    }
}
technique11 Light1FogNT
{
    pass P0
    {
        SetVertexShader( CompileShader( vs_4_0, VS_NT() ) );
        SetGeometryShader( NULL );
        SetPixelShader( CompileShader( ps_4_0, PS(1, true) ) );
    }
}
technique11 Light2FogNT
{
    pass P0
    {
        SetVertexShader( CompileShader( vs_4_0, VS_NT() ) );
        SetGeometryShader( NULL );
        SetPixelShader( CompileShader( ps_4_0, PS(2, true) ) );
    }
}
technique11 Light3FogNT
{
    pass P0
    {
        SetVertexShader( CompileShader( vs_4_0, VS_NT() ) );
        SetGeometryShader( NULL );
        SetPixelShader( CompileShader( ps_4_0, PS(3, true) ) );
    }
}

Next Time…

As promised earlier, we will cover how to generate random terrains using procedural techniques.  The method presented will be relatively simple, using Perlin Noise to generate a random heightmap, with some filtering techniques to produce a smoother terrain.  We will also look at how to generate a simple blend map to match the random heightmap, selecting the terrain texture based on the height of the terrain.