Mazes in C# - Part 1

Data Representation

The easiest way to model a maze is as a 2D rectangular grid of cells.

Cell

The first step is to define the structure that we will use to represent each cell in our maze grid. There are a few pieces of information that we need to keep track of:

• The XY position of the cell in the maze.
• The cells which neighbor this cell (north, south, east and west).
• The cells which are linked to this cell. Cells are linked if there is a path between them. For simplicity, we'll only record the cells which are linked to this cell, otherwise assuming that any other cells are not linked.

public class Cell {
    // Position in the maze
    public int Row { get; }
    public int Column { get; }

    // Neighboring cells
    [CanBeNull]
    public Cell North { get; set; }
    [CanBeNull]
    public Cell South { get; set; }
    [CanBeNull]
    public Cell East { get; set; }
    [CanBeNull]
    public Cell West { get; set; }

    public List<Cell> Neighbors {
        get { return new[] { North, South, East, West }.Where(c => c != null).ToList(); }
    }

    // Cells that are linked to this cell
    private readonly Dictionary<Cell, bool> _links;
    public List<Cell> Links => _links.Keys.ToList();

    public Cell(int row, int col) {
        Row = row;
        Column = col;
        _links = new Dictionary<Cell, bool>();
    }
    // ...
}

You can ignore the [CanBeNull] annotations if you like - these are just some hints for the ReSharper static analyzer.

We'll also define some utility functions which will serve to link and unlink cells, and to test whether two cells are linked. Our linking functions will also handle making sure that links are bidirectional, although with the option of making one-way links. For now, we're not going to make much use of this, but one can imagine that if we extend our map to include one-way connections, like chutes between levels, that will come in handy.

    public void Link(Cell cell, bool bidirectional = true) {
        _links[cell] = true;
        if (bidirectional) {
            cell.Link(this, false);
        }
    }

    public void Unlink(Cell cell, bool bidirectional = true) {
        _links.Remove(cell);
        if (bidirectional) {
            cell.Unlink(this, false);
        }
    }

    public bool IsLinked(Cell cell) {
        if (cell == null) {
            return false;
        }
        return _links.ContainsKey(cell);
    }

Grid

With the Cell data structure taken care of, we can move onto our Grid class. This will consist of:

• Dimensions of the grid.
• The 2D array of Cells - here we will use a nested List<T> for convenience.
• Accessors that will allow us to index a Cell by its XY coordinates, a random Cell accessor, and iterators that will allow us to access Cells by row or one-by-one.
• Helper functions to initialize the grid, and setup the neighbors for each cell.

public class Grid {
    public int Rows { get; }
    public int Columns { get; }
    public int Size => Rows * Columns;

    private List<List<Cell>> _grid;

    [CanBeNull]
    public virtual Cell this[int row, int column] {
        get {
            if (row < 0 || row >= Rows) {
                return null;
            }
            if (column < 0 || column >= Columns) {
                return null;
            }
            return _grid[row][column];
        }
    }
    [NotNull]
    public Cell RandomCell() {
        var rand = new Random();
        var row = rand.Next(Rows);
        var col = rand.Next(Columns);
        var randomCell = this[row, col];
        if (randomCell == null) {
            throw new InvalidOperationException("Random cell is null");
        }
        return randomCell;
    }
    // Row iterator
    public IEnumerable<List<Cell>> Row {
        get {
            foreach (var row in _grid) {
                yield return row;
            }
        }
    }
    // Cell iterator
    public IEnumerable<Cell> Cells {
        get {
            foreach (var row in Row) {
                foreach (var cell in row) {
                    yield return cell;
                }
            }
        }
    }

    public Grid(int rows, int cols) {
        Rows = rows;
        Columns = cols;

        PrepareGrid();
        ConfigureCells();
    }

    private void PrepareGrid() {
        _grid = new List<List<Cell>>();
        for (var r = 0; r < Rows; r++) {
            var row = new List<Cell>();
            for (var c = 0; c < Columns; c++) {
                row.Add(new Cell(r, c));
            }
            _grid.Add(row);
        }
    }

    private void ConfigureCells() {
        foreach (var cell in Cells) {
            var row = cell.Row;
            var col = cell.Column;

            cell.North = this[row - 1, col];
            cell.South = this[row + 1, col];
            cell.West = this[row, col - 1];
            cell.East = this[row, col + 1];
        }
    }
    // ...
}

Displaying the Grid

At this point, we can setup and represent a grid for a maze, but we really need a way to output this grid in a way that makes it easy to visualize. As a first step, we'll override the .NET ToString() method to render the grid in ASCII, which is helpful for outputting to the console with small mazes.

public override string ToString() {
    var output = new StringBuilder("+");
    for (var i = 0; i < Columns; i++) {
        output.Append("---+");
    }
    output.AppendLine();

    foreach (var row in Row) {
        var top = "|";
        var bottom = "+";
        foreach (var cell in row) {
            const string body = "   ";
            var east = cell.IsLinked(cell.East) ? " " : "|";

            top += body + east;

            var south = cell.IsLinked(cell.South) ? "   " : "---";
            const string corner = "+";
            bottom += south + corner;
        }
        output.AppendLine(top);
        output.AppendLine(bottom);
    }

    return output.ToString();
}

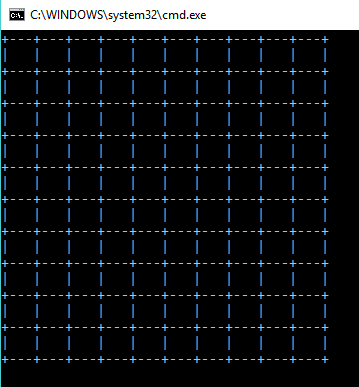
Here is what that looks like with our initialized grid, before we have started connecting any cells:

This is pretty basic - we could fancy things up by using some Unicode or extended ASCII block characters, but it's good enough for debugging purposes. What would be more interesting is rendering the maze as an image, which we will do next, using some simple WinForms graphics commands.

public Image ToImg(int cellSize = 50) {
    var width = cellSize * Columns;
    var height = cellSize * Rows;

    var img = new Bitmap(width, height);
    using (var g = Graphics.FromImage(img)) {
        g.Clear(Color.White);
        foreach (var cell in Cells) {
            var x1 = cell.Column * cellSize;
            var y1 = cell.Row * cellSize;
            var x2 = (cell.Column + 1) * cellSize;
            var y2 = (cell.Row + 1) * cellSize;


            if (cell.North == null) {
                g.DrawLine(Pens.Black, x1, y1, x2, y1);
            }
            if (cell.West == null) {
                g.DrawLine(Pens.Black, x1, y1, x1, y2);
            }

            if (!cell.IsLinked(cell.East)) {
                g.DrawLine(Pens.Black, x2, y1, x2, y2);
            }
            if (!cell.IsLinked(cell.South)) {
                g.DrawLine(Pens.Black, x1, y2, x2, y2);
            }
        }
    }


    return img;
}

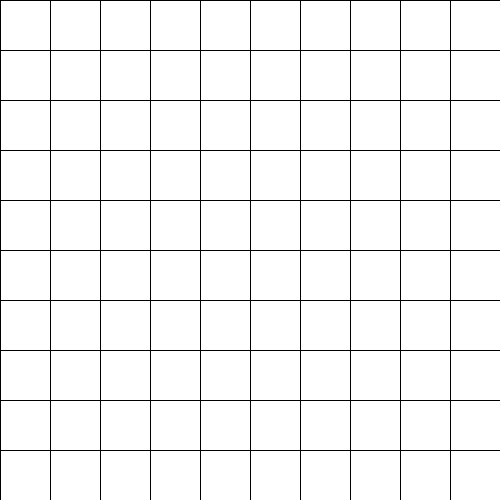
This is a little nicer:

List Sampling Extension

One final bit of infrastructure that will make our subsequent code easier is an extension method that will randomly select an element from a List<T>

public static class ListExtensions {
    public static T Sample(this List list, Random rand = null) {
        if (rand == null) {
            rand = new Random();
        }
        return list[rand.Next(list.Count)];
    }
}

The Maze Algorithms

With those foundations out of the way, we can start implementing some algorithms to actually create mazes on our Grid. We're going to start with two very simple algorithms, the Binary Tree and Sidewinder algorithms. These algorithms are very fast and simple to implement, and require very minimal state - although they do have some disadvantages, as we will see.

NOTE: If you examine the code on GitHub, these algorithm classes are somewhat more complicated than shown here - they include some additional logic that makes it possible to run the algorithms one step at a time, which is handy for visualizing how the algorithms work.

Binary Tree Algorithm

The Binary Tree algorithm is very simple. For each cell in the grid:

1. Take the neighboring cells to the north and east, ignoring null cells (i.e., on the top row of the grid, northern neighbors don't exist, and likewise for the eastern neighbors on the right-hand edge of the grid).
2. Pick one of the available options randomly. If there are no options, move on to the next cell.
3. Link the current cell to the chosen neighbor.
4. Move on to the next cell.

public class BinaryTree : IMazeAlgorithm {
    // ...
    public static Grid Maze(Grid grid, int seed = -1) {
        var rand = seed >= 0 ? new Random(seed) : new Random();
        foreach (var cell in grid.Cells) {
            var neighbors = new[] { cell.North, cell.East }.Where(c => c != null).ToList();
            if (!neighbors.Any()) {
                continue;
            }
            var neighbor = neighbors.Sample(rand);
            if (neighbor != null) {
                cell.Link(neighbor);
            }
        }
        return grid;
    }
    // ...
}

Here you can see the Binary Tree algorithm proceeding step-by-step. There's a couple things to note about this algorithm.

• It only needs to visit each cell in the grid once - thus it is O(n) with respect to the number of cells in the grid. It also doesn't need to maintain any state or allocate any additional memory.
• There's a strong diagonal bias to the paths running from the northeast corner towards the southwest corner or vice versa. This is a consequence of the way the neighboring cells to link were chosen. In fact, if we consider the northeast corner and work towards through the connections, we will form a binary search tree (hence the name), with the northeast corner as the root, and the southwest corner as the deepest leaf.
• Similarly, it is impossible to move north or west into a dead end.
• The northernmost row and easternmost column of the grid will always be open.

Sidewinder Algorithm

The Sidewinder algorithm is very similar to Binary Tree, albeit with a few tweaks that reduce some of the biases evidenced by the Binary Tree algorithm. Instead of considering every cell independently, we will have to maintain a bit of state to keep track of the last run of cells in the row that we have processed. Starting with the western-most cell in each row:

1. If we are in the northernmost row, connect this cell with it's eastern neighbor.
2. Otherwise, add this cell to the run of cells that we have processed in this row so far.
   1. Chose between connecting this cell with its eastern neighbor, or connecting one of the cells in the run of previous cells to its northern neighbor.
   2. If we connect northward, clear the run of previously processed cells.
   3. Move on to the next cell in the row.
3. Move on to the next row.

public class Sidewinder : IMazeAlgorithm {
    // ...
    public static Grid Maze(Grid grid, int seed = -1) {
        var rand = seed >= 0 ? new Random(seed) : new Random();
        foreach (var row in grid.Row) {
            var run = new List();

            foreach (var cell in row) {
                run.Add(cell);

                var atEasternBoundary = cell.East == null;
                var atNorthernBoundary = cell.North == null;

                var shouldCloseOut = atEasternBoundary || (!atNorthernBoundary && rand.Next(2) == 0);

                if (shouldCloseOut) {
                    var member = run.Sample(rand);
                    if (member.North != null) {
                        member.Link(member.North);
                    }
                    run.Clear();
                } else {
                    cell.Link(cell.East);
                }
            }
        }
        return grid;
    }
    // ...
}

This is easier to see than to describe in words, but roughly what we are doing is, instead of choosing to go north or east at every cell, we chose between going east, or going north from somewhere in a block of east-west connected cells.

• This still means that we are processing each cell once, and are thus O(n). We are using a bit of additional memory to store the run of previous cells in the row. All in all, this is still a very fast algorithm.
• It is now possible to move west into a dead end. However, it is still impossible to hit a dead end going north.
• While the eastern column is no longer open, the northern row is still an open corridor.
• Instead of a diagonal northeast-southwest bias, we have a somewhat more subtle north-south bias. From any point, there will only be one northern connection that you can reach.

To close, here are the results of the two maze generation algorithms, with Binary Tree on the left and Sidewinder on the right, for comparison's sake. Included in the project on GitHub is a small WinForms app that allows stepping through the algorithms step-by-step, changing the random seed, and saving the mazes out to an image - feel free to play around with it.

This has been fun; I'm hoping I'll have time this week to move a little further and write up another post on the next chapter or two and get into implementing Dijkstra's algorithm, as well as some of the more advanced maze generation algorithms.

P.S. I would recommend vacationing at Long Bay, Antigua. The Pineapple Beach Club was beautiful