CLRS Algorithm a Day: Insertion Sort
The other day I was on HackerNews lurking as I do, and there were a number of people praising Introduction to Algorithms, the infamous CLRS book. Almost everybody who has been through a Computer Science degree has had to buy a copy of it and slog along through at some point. It's basically the bible of algorithms and data structures classes, and as most of that kind of book are, it's a weighty tome that costs about a week's work-study wages. Mine has mostly been gathering dust on the shelf for the past ten years...

I've got a little bit of a love-hate relationship with the book. My algorithms and data structures class in college was entirely theoretical - we didn't write a single line of code during the whole semester, we just did page after page of proofs. Moreover, the professor was one of those space-case academic types, who was probably a bang-up researcher, but couldn't teach a lick. My only enduring memories of that course are chalk scratching on the blackboard, as she transcribed the textbook word for word and symbol for symbol, and sitting in the 1902 Room in Baker Library with reams of scratch paper scattered across the table, flailing away doing induction proofs. Oh, and the week we spent going over that median-of-medians algorithm that I've still never seen a point to... I think I scratched out a B-, and it was easily the least enjoyable class of my entire degree.
On the other hand, I could see that there was a lot of really cool information in the text, if it was taught differently. I always thought that a hands-on version of the class, where you had to implement everything in C, rather than pseudocode and pencil, would be really fun, and moreover, really teach people how to program. Alas, we skipped a lot of the interesting material in the book, and overwhelmingly focused on proving run-time complexity bounds. Which I always thought was a little dumb, detached from real-life implementation details - there was very little consideration of trading space for time, or taking into account the capabilities of the hardware, or other real life concerns - but that is neither here nor there.
So this week, I decided to dust off my copy and give it another go. I'm mostly a C# programmer, and probably will remain one for the foreseeable future; it's a really nice language. However, I'm going to try to keep things pretty basic for the most part, to hew as closely to the pseudocode presented in the text.
Insertion Sort
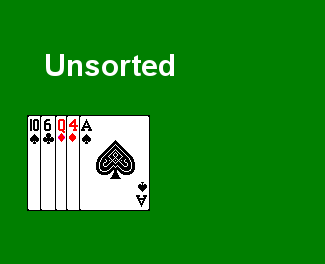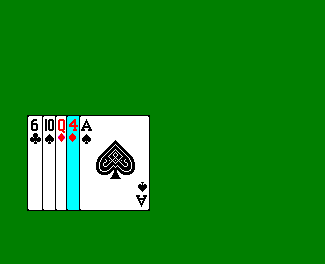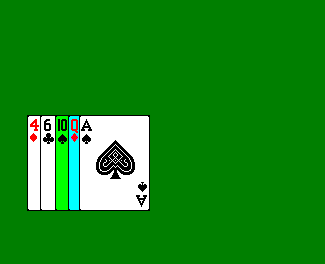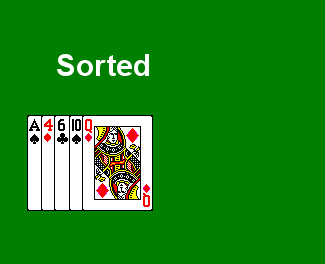
The first algorithm presented in the book is one of the elementary examples, Insertion Sort. This is a simple in-place sorting algorithm. Conceptually, this is very similar to the way that many people sort their hand in a game of cards. If we are dealt five cards:
- Start with the first card. The first card is implicitly sorted, if we consider that this constitutes a sub-array of one card.
- Now we consider the second card. If it is greater than the first card, we can leave it where it is, and now have a 2-card sorted sub-array. Otherwise, we insert it to the left of the first card, which also gives us a two-card sorted sub-array.
- Now consider the third card. We take this card, and insert it into the correct position, relative to the two left sorted cards, so that the three-card array is sorted, shifting cards to the right if necessary.
- We continue on in this fashion for the fourth and fifth cards.
There are a few interesting properties of this algorithm to observe:
- When we consider the first card, it is comprises a single element subarray, which is automatically sorted.
- When we consider a subsequent card n, we already have cards 1 .. n-1 to the left in a sorted sub-array. So our only task is then to insert card n into the correct position in that sorted sub-array. Once we have done this, this yields a sorted sub-array of cards 1 .. n when we go to consider card n+1.
- The card that we are considering always sweeps to the right monotonically, without having to backtrack into the lefthand sorted sub-array once it is sorted.
- In the best case, with an already-sorted array, we will only need to compare each element with its preceding element, which gives a best-case runtime of O(n).
- However, in the worst-case, that of a reverse-sorted array, for every single element, we will need to compare and shift it against every previously sorted element, yielding a worst-case runtime of O(n2).
Pseudocode
The original (vaguely Pythonic) pseudocode from CLRS is:
InsertionSort(A)
for j = 2 to A.length
key = A[j]
i = j - 1
while i > 0 and A[j] > key
A[i+1] = A[i]
i = i - 1
A[i+1] = key
Naive Implementation
Translating this into C# code is relatively straightforward, the biggest change being that arrays in C# are 0-based, rather than 1-based as in the CLRS pseudocode dialect. I've also written this as an extension method, for convenience when calling the InsertionSort method.
public static void InsertionSort(this int[] a) {
for (var j = 1; j < a.Length; j++) {
var key = a[j];
var i = j - 1;
while (i >= 0 && a[i] > key) {
a[i + 1] = a[i];
i--;
}
a[i + 1] = key;
}
}We can write some quick NUnit tests, leveraging the IEnumerable.SequenceEqual method to verify that this code is working correctly (the third case is the same as the example shown in the GIF above):
[TestCase(new[] { 1, 2, 3 }, new[] { 1, 2, 3 }, TestName = "In Order")]
[TestCase(new[] { 2, 3, 1 }, new[] { 1, 2, 3 }, TestName = "Out of Order")]
[TestCase(new[] { 10, 6, 12, 4, 1 }, new[] { 1, 4, 6, 10, 12 }, TestName = "Card Example")]
public void SortInPlace(int[] input, int[] expected) {
var sorted = input;
input.InsertionSort();
Assert.True(sorted.SequenceEqual(expected));
}Sorting more kinds of things with generics
Sorting arrays of integers is great, but this code won't work if we want to sort an array of floats, or an array of string, or an array of some other kind of data. Fortunately, C# has some good support for generic typing, so we can easily write a version of this method that will work on any type that implements the IComparable<T> interface. This interface is supported by most of the built-in value types in .NET, as well as many other types of objects.
public static void InsertionSort<T>(this T[] a) where T : IComparable<T> {
for (var j = 1; j < a.Length; j++) {
var key = a[j];
var i = j - 1;
while (i >= 0 && a[i].CompareTo(key) > 0) {
a[i + 1] = a[i];
i--;
}
a[i + 1] = key;
}
}The many ways to compare in .NET
This is a very helpful refinement, and works very well for most cases; however, it does have the caveat that it requires the type that makes up your array to implement the IComparable<T> interface. Ideally, this would always be the case, but we don't always go to the full effort of designing classes to support all of the interfaces that would be helpful, or are using third-party types that we don't control. Or perhaps we simply want to sort differently than the default comparison operation provided by the IComparable interface.
The classic way to implement such a more flexible sorting method would be to pass in an instance of an IComparer<T> object, which is then used to do the comparison in the while loop:
public static void InsertionSort<T>(this T[] a, IComparer<T> comparer) {
for (var j = 1; j < a.Length; j++) {
var key = a[j];
var i = j - 1;
while (i >= 0 && comparer.Compare(a[i], key) > 0) {
a[i + 1] = a[i];
i--;
}
a[i + 1] = key;
}
}Having to define and instantiate IComparer objects is kind of a drag, so another common strategy is to use a delegate function instead. Alas, full-on delegates are also something of a drag, so as of .NET 3.5, inspired by their widespread use in LINQ, we have been able to use the Func<T> lambda functions instead, which makes this much cleaner, e.g.:
public static void InsertionSort<T>(this T[] a, Func<T,T, bool> greaterThan) {
for (var j = 1; j < a.Length; j++) {
var key = a[j];
var i = j - 1;
while (i >= 0 && greaterThan(a[i], key)) {
a[i + 1] = a[i];
i--;
}
a[i + 1] = key;
}
}This is quite slick to use, as we can see from this set of tests:
[TestCase(new[] { 1, 2, 3 }, new[] { 1, 2, 3 }, TestName = "In Order")]
[TestCase(new[] { 2, 3, 1 }, new[] { 1, 2, 3 }, TestName = "Out of Order")]
[TestCase(new[] { 10, 6, 12, 4, 1 }, new[] { 1, 4, 6, 10, 12 }, TestName = "Card Example")]
public void SortInPlaceFunc(int[] input, int[] expected) {
var sorted = input;
input.InsertionSort((a, b) => a > b);
Assert.True(sorted.SequenceEqual(expected));
}But the real power of this technique comes in if we want to use a custom sorting order. Like, for instance, if we wanted to sort the items in decreasing order, instead of ascending:
[TestCase(new[] { 1, 2, 3 }, new[] { 3, 2, 1 }, TestName = "In Order")]
[TestCase(new[] { 2, 3, 1 }, new[] { 3, 2, 1 }, TestName = "Out of Order")]
[TestCase(new[] { 10, 6, 12, 4, 1 }, new[] { 12, 10, 6, 4, 1 }, TestName = "Card Example")]
public void SortInPlaceFuncDesc(int[] input, int[] expected) {
var sorted = input;
input.InsertionSort((a, b) => a < b);
Assert.True(sorted.SequenceEqual(expected));
}The history and development of the C# language over the years has left this legacy of different ways of doing things... If this interests you, I highly recommend checking out Jon Skeet's excellent C# in Depth, which digs deep into this evolution. But for practical purposes, it is enough to provide the IComparable<T> and Func<T, T, bool> variants, in modern C#. This gives all of the power of using generics, with 1.) reasonable default behavior, and 2.) custom behavior for where it is needed.
Immutable/Fluent Sort
Although InsertionSort is a designed as an in-place algorithm, i.e. it operates on the passed in array and modifies it, sometimes it is desirable to instead return a sorted copy of the original array, without destroying the original ordering. Note that this does consume extra memory, as it is necessary to create that copy that is returned, in addition to the source array. This sort of pattern is also common in so-called fluent APIs, such as the method-chaining style of LINQ (foo.Where(f=>f>3).Select(f=>f*f).OrderBy(f=>f)).
public static T[] InsertionSorted<T>(T[] a) where T : IComparable<T> {
var ret = a.ToArray(); // use the ToArray() method to create a new, copy of the original array
ret.InsertionSort();
return ret;
}Recursive Insertion Sort
Lastly, it's an interesting exercise to convert this algorithm to run recursively, rather than iteratively. There's not really much point in doing so, unless you delight in confusing your coworkers, or desire to run into stack overflow issues on very large arrays. I'll leave that exercise to the reader, although if you are curious, there's an implementation in the GitHub repository for this post https://github.com/ericrrichards/algorithms