Mazes in C# - Part 2 - Dijkstra's Algorithm
Last time, I had started working through Jamis Buck's Mazes for Programmers. I've made quite a lot of progress in the meantime, but haven't managed to keep up with posting about that progress. Today, we're going to work through the meat of Chapter 3, where we'll implement a simplified version of Dijkstra's Algorithm (really a breadth-first search), which we'll use to find paths through our mazes. We will also use this algorithm to help visualize the biases that exist in our two previous maze generation algorithms, by coloring the backgrounds of each cell according to its distance from a starting point.
You can download the code for this post by downloading or cloning the Post_2 branch from my GitHub. Going forward, I'm going to try and tag the code for each post in a new branch - I'm still used to the old SVN model, but I'm trying to figure out how to take advantage of Git a little more.
Below you can see an example of where we'll end up, drawing the longest path through a maze, and coloring each cell according to its distance along the path.
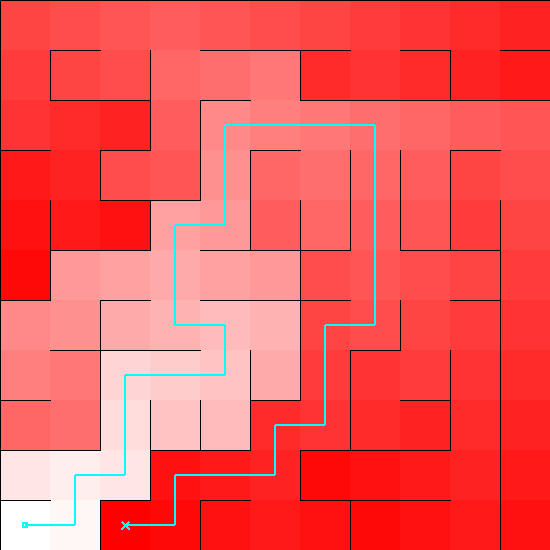
Let's get started!
Simplified Dijkstra's Algorithm
Edsger Dijkstra was an early Dutch computer scientist, who made a huge number of contributions to computer science. Besides the shortest-path graph theory algorithm which we are going to implement today, he was a pioneer in concurrent programming, a driving force behind the ALGOL programming language (one of the progenitors of C, and everything that has followed it), as well as an early proponent of structured programming, which nearly all modern programming languages implement. We also have him to thank (in addition to Niklaus Wirth) for the hundreds or thousands of "X considered harmful" articles and blog posts that have proliferated in the decades since he penned the iconic Go To Statement Considered Harmful in 1968.
Dijkstra's Algorithm is a fairly simple, but very powerful algorithm that is widely used in pathfinding applications. This algorithm is very effective for finding shortest paths in any kind of graph structure, not just square grids, provided that all of the edges between nodes in the graph have costs greater than zero - which for most applications is always the case. I've already covered one derivative of Dijkstra's in my DirectX series, the A* algorithm. Essentially, Dijkstra's Algorithm works its way outward from its starting point, selecting the shortest path to the goal point by selecting the next unvisited cell with the lowest cumulative path cost. For simplicity's sake, we're going to assume that all of the edges in our maze have a cost of one (which makes this effectively a Breadth-First Search) - later on, we'll revisit this, and build a more general version that can handle arbitrary costs to move between cells.
Step by step, the algorithm works like this:
- Assign all of the cells in the maze a distance of -1. We will consider all cells that have a distance less than 0 to be unvisited
- Take the starting cell, and assign it a distance of zero. We also add the starting cell to a set of cells that we will call the frontier.
-
While there are still cells in the frontier set, create a new frontier set, and then loop over the cells in the frontier set.
- For each cell in the frontier, take the neighbors of the current cell that have not been visited yet (that have a distance of -1), and set their distance to the distance of the current cell plus one, and then add them to the new frontier set, if it is not already present in the new frontier set.
- Once we have looped over all the cells in the original frontier list, replace the original frontier set with the new frontier set, and continue until all the cells have been visited. This will give us the distance from the starting cell to every other cell (Remember, these are perfect mazes, so every cell is reachable from every other cell).
Implementing Dijkstra's
We'll start by defining the data structure that will store the matrix of distances from a start cell to every other cell in the maze. This will consist of:
- The root starting cell
- A Dictionary mapping cells to their distance from the start cell
- An accessor that gives us the cells that are present in the dictionary
- A constructor, which initializes the root cell, and adds it to the distances dictionary with a distance of zero.
- An indexer, which will allow us to query the distance of a cell in the grid from the start point. Note that we need to check that the cell is contained in the dictionary, and if it is not, we will return our sentinel -1 distance. We will also be able to set the distance of a cell using this indexer.
public class Distances {
private Cell Root { get; }
private readonly Dictionary<Cell, int> _cells;
public List<Cell> Cells => _cells.Keys.ToList();
public Distances(Cell root) {
Root = root;
_cells = new Dictionary<Cell, int> { { Root, 0 } };
}
public int this[Cell cell] {
get {
if (_cells.ContainsKey(cell)) {
return _cells[cell];
}
return -1;
}
set => _cells[cell] = value;
}
// more later...
}Next, we'll add an implementation of Dijkstra's algorithm to our Cell class from last time, to compute the distances from this cell to all the other cells in the grid, following the algorithm we laid out above.
public class Cell {
// previous implementation omitted...
public Distances Distances {
get {
var distances = new Distances(this);
var frontier = new HashSet<Cell> {
this
};
while (frontier.Any()) {
var newFrontier = new HashSet<Cell>();
foreach (var cell in frontier) {
foreach (var linked in cell.Links) {
if (distances[linked] >= 0) {
continue;
}
distances[linked] = distances[cell] + 1;
newFrontier.Add(linked);
}
}
frontier = newFrontier;
}
return distances;
}
}
}And that's that, we've implemented Dijkstra's Algorithm for our mazes. However, at present, this isn't terribly useful, without any way to visualize that distance information. We'll start with a very simple way to show this information, by creating a subclass of our Grid class that will display these distances in our textual console output.
DistanceGrid Class
To add the ability to print out the distance of a cell from the starting point, we're going to have to revisit our Grid class from last time and do a little refactoring to our ToString() method. We'll add a virtual method that can be overridden in subclasses to control how the content of a cell is rendered, using some nifty C# 6.0 string interpolation.
public class Grid {
// other implementation omitted...
protected virtual string ContentsOf(Cell cell) {
return " ";
}
public override string ToString() {
var output = new StringBuilder("+");
for (var i = 0; i < Columns; i++) {
output.Append("---+");
}
output.AppendLine();
foreach (var row in Row) {
var top = "|";
var bottom = "+";
foreach (var cell in row) {
var body = $" {ContentsOf(cell)} ";
var east = cell.IsLinked(cell.East) ? " " : "|";
top += body + east;
var south = cell.IsLinked(cell.South) ? " " : "---";
const string corner = "+";
bottom += south + corner;
}
output.AppendLine(top);
output.AppendLine(bottom);
}
return output.ToString();
}
}This allows us to easily create a new subclass that will render the maze with the distance information, the DistanceGrid
public class DistanceGrid : Grid {
public Distances Distances { get; set; }
public DistanceGrid(int rows, int cols) : base(rows, cols) { }
protected override string ContentsOf(Cell cell) {
if (Distances != null && Distances[cell] >= 0) {
return Distances[cell].ToBase64();
}
return base.ContentsOf(cell);
}
}In a grid of any size, we will end up with distances greater than we can show with a single integer character, and rather than deal with trying to justify the output, I created a silly little extension method to convert an integer to base-64, as well as one to convert to base-36 (0-9, a-z).
public static class IntExtensions {
public static string ToBase36(this int i) {
const string chars = "0123456789abcdefghijklmnopqrstuvwxyz";
return chars[i % 36].ToString();
}
public static string ToBase64(this int i) {
const string chars = "0123456789abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ%=";
return chars[i % 64].ToString();
}
}We can then use this DistanceGrid class to generate and output a maze with distance information:
var distGrid = new DistanceGrid(10,10);
BinaryTree.Maze(distGrid);
var start = distGrid[0, 0];
var distances = start.Distances;
distGrid.Distances = distances;
Console.WriteLine(distGrid);Which yields:
+---+---+---+---+---+---+---+---+---+---+ | 0 1 2 3 4 5 6 7 8 9 | +---+---+ +---+---+---+ +---+---+ + | 5 4 3 | a 9 8 7 | c b a | + + +---+ +---+ + +---+ + + | 6 | 5 | c b | a 9 | 8 | d c | b | +---+---+---+---+ + + +---+ + + | f e d c b | a | 9 | e d | c | +---+ +---+---+---+---+ +---+---+ + | g f | e d c b a | f e d | + +---+---+---+ + + +---+ + + | h | g f e d | c | b | g f | e | +---+---+---+---+ +---+---+---+ + + | i h g f e | j i h g | f | +---+---+---+ + + + + + + + | j i h g | f | k | j | i | h | g | + + +---+---+---+---+ + + + + | k | j | o n m l k | j | i | h | +---+ +---+ +---+ +---+ + + + | l k | p o | n m | l k | j | i | +---+---+---+---+---+---+---+---+---+---+
This is all well and good, but it's not very pretty! Next, we'll create another subclass that will render our mazes as images, with the color of each cell shaded by the distance from the start.
ColoredGrid Class
Once again, we'll need to go back to our Grid class and do some refactoring, this time to the ToImg() method. We'll change this method so that it draws each cell in two passes: the background color for each cell, which is new, and the walls of the cell, which will remain the same as before. To do this, we'll add a new enum type to represent these different drawing stages, and we'll also add another virtual method which will return the color that a cell should be filled with, which we can override in derived classes.
public class Grid {
// other implementation omitted...
private enum DrawMode {
Background, Walls
}
protected virtual Color? BackgroundColorFor(Cell cell) {
return null;
}
public Image ToImg(int cellSize = 50) {
var width = cellSize * Columns;
var height = cellSize * Rows;
var img = new Bitmap(width, height);
using (var g = Graphics.FromImage(img)) {
g.Clear(Color.White);
foreach (var mode in new[]{DrawMode.Background, DrawMode.Walls}) {
foreach (var cell in Cells) {
var x1 = cell.Column * cellSize;
var y1 = cell.Row * cellSize;
var x2 = (cell.Column + 1) * cellSize;
var y2 = (cell.Row + 1) * cellSize;
if (mode == DrawMode.Background) {
var color = BackgroundColorFor(cell);
if (color != null) {
g.FillRectangle(new SolidBrush(color.GetValueOrDefault()), x1, y1, cellSize, cellSize );
}
} else if (mode == DrawMode.Walls) {
if (cell.North == null) {
g.DrawLine(Pens.Black, x1, y1, x2, y1);
}
if (cell.West == null) {
g.DrawLine(Pens.Black, x1, y1, x1, y2);
}
if (!cell.IsLinked(cell.East)) {
g.DrawLine(Pens.Black, x2, y1, x2, y2);
}
if (!cell.IsLinked(cell.South)) {
g.DrawLine(Pens.Black, x1, y2, x2, y2);
}
}
}
}
}
return img;
}
}Then we will create a subclass that will implement the colorization based on distance, the ColoredGrid class.
public class ColoredGrid : Grid {
private Distances _distances;
private Cell _farthest;
private int _maximum;
public ColoredGrid(int rows, int cols) : base(rows, cols) {
BackColor = Color.Green;
}
public Color BackColor { get; set; }
public Distances Distances {
get => _distances;
set {
_distances = value;
(_farthest, _maximum) = value.Max;
}
}
protected override Color? BackgroundColorFor(Cell cell) {
if (Distances == null || Distances[cell] < 0) {
return null;
}
var distance = Distances[cell];
var intensity = (_maximum - distance) / (float)_maximum;
return BackColor.Scale(intensity);
}
}.Net doesn't have a convenient function for scaling a color, so I implemented another extension method to do this scaling. There is also an additional extension method to invert a color, which will come in handy shortly.
public static class ColorExtensions {
public static Color Scale(this Color color, float intensity) {
return Color.FromArgb(
(int)(color.R + (255-color.R) * intensity),
(int)(color.G + (255 - color.G) * intensity),
(int)(color.B + (255 - color.B) * intensity)
);
}
public static Color Invert(this Color color) {
return Color.FromArgb(color.ToArgb() ^ 0xffffff);
}
}Now, armed with the ColoredGrid class, we can generate some pretty images. Below shows mazes generated with the Binary Tree and Sidewinder algorithms, left and right.
With the mazes colorized like this, the biases in the Binary Tree and Sidewinder algorithms become very evident. The Binary Tree algorithm exhibits a strong diagonal grain, running from the northeast to the southwest, while the Sidewinder has a pronounced north-south grain. Both of these are artifacts of the constraints that these algorithms place on neighboring cell selection as they carve passages. As we implement more maze algorithms, we'll continue making use of this color visualization to analyze the biases of each additional algorithm.
Drawing Paths
The last thing that we are going to do is add some functionality to our Distances class for computing the path between two cells, and for finding the longest path in a maze. We're also going to subclass our Grid class once again, so that it will support drawing paths when we render it as an image.
Calculating Paths
Our Distances class currently calculates the distances from a start cell to every other cell in the maze. With a little work, we can extend this class to also allow us to calculate the shortest path from the start cell to a goal cell. We'll do this by generating the distances information outward from the start cell, and then walking backwards from the goal cell, taking advantage of the property that the distance of the next cell in the path will always be less than the current distance. As we build up the path, working backwards, we will add to a new Distances instance, which will end up containing information for just the cells along the path.
public class Distances {
// other implementation omitted...
public Distances PathTo(Cell goal) {
var current = goal;
var breadcrumbs = new Distances(Root) {
[current] = _cells[current]
};
while (current != Root) {
foreach (var neighbor in current.Links) {
if (_cells[neighbor] < _cells[current]) {
breadcrumbs[neighbor] = _cells[neighbor];
current = neighbor;
break;
}
}
}
return breadcrumbs;
}
}Using our DistanceGrid which we implemented earlier, we can see how this works, drawing a path from the northwest corner to the southeast corner of a Binary Tree maze:
var distGrid = new DistanceGrid(10,10);
BinaryTree.Maze(distGrid);
var start = distGrid[0, 0];
var distances = start.Distances;
distGrid.Distances = distances.PathTo(distGrid[distGrid.Rows-1, 0]);
Console.WriteLine(distGrid);Which yields:
+---+---+---+---+---+---+---+---+---+---+ | 0 1 2 3 4 5 6 | +---+---+ +---+---+---+ +---+---+ + | | 7 | | + + +---+ +---+ + +---+ + + | | | | | 8 | | | +---+---+---+---+ + + +---+ + + | | | 9 | | | +---+ +---+---+---+---+ +---+---+ + | | c b a | | + +---+---+---+ + + +---+ + + | | d | | | | | +---+---+---+---+ +---+---+---+ + + | f e | | | +---+---+---+ + + + + + + + | i h g | | | | | | | + + +---+---+---+---+ + + + + | | j | | | | | +---+ +---+ +---+ +---+ + + + | l k | | | | | | +---+---+---+---+---+---+---+---+---+---+
Finding the longest path
It can also be useful to determine what the longest path through a maze is. Although Dijkstra's algorithm is primarily useful for finding the shortest path through a maze, because our Distances class computes the distance from the start to every other cell, we can leverage that information to find the longest path by running the algorithm twice - once to find the cell that is the farthest from an original starting point, and then running it again to find the farthest cell from that point. To do this, we'll need to add a method to our Distances class that will return the most distant cell from our start point. This is a pretty straight-forward case of looping over the cells to find the most distant cell:
public class Distances {
// other implementation omitted...
public (Cell maxCell, int maxDistance) Max {
get {
var maxDistance = 0;
var maxCell = Root;
foreach (var cell in _cells) {
if (cell.Value > maxDistance) {
maxDistance = cell.Value;
maxCell = cell.Key;
}
}
return (maxCell, maxDistance);
}
}Using this Max method to find the longest path in a grid is fairly easy:
var longestGrid = new DistanceGrid(10,10);
BinaryTree.Maze(longestGrid);
var start = longestGrid[0, 0];
var distances = start.Distances;
var (newStart, distance) = distances.Max;
var newDistances = newStart.Distances;
var (goal, distance2) = newDistances.Max;
longestGrid.Distances = newDistances.PathTo(goal);
Console.WriteLine(longestGrid);Which yields:
+---+---+---+---+---+---+---+---+---+---+ | j i h g | +---+---+ +---+---+---+ +---+---+ + | | k | f | + + +---+ +---+ + +---+ + + | | | | | l | | e | +---+---+---+---+ + + +---+ + + | | | m | | d | +---+ +---+---+---+---+ +---+---+ + | | p o n | b c | + +---+---+---+ + + +---+ + + | | q | | | a | | +---+---+---+---+ +---+---+---+ + + | s r | 7 8 9 | | +---+---+---+ + + + + + + + | v u t | | | 6 | | | | + + +---+---+---+---+ + + + + | | w | 2 3 4 5 | | | | +---+ +---+ +---+ +---+ + + + | y x | 0 1 | | | | | +---+---+---+---+---+---+---+---+---+---+
Drawing paths
With this infrastructure in place, it is only a little more work to add another subclass of our Grid class that is capable of drawing paths in its ToImg() method. Once again, we're going to add a bit of functionality to our Grid class to facilitate this. We'll add another drawing mode to our enum, and add another virtual method to delegate the actual drawing of the path to any subclasses that we choose to implement it in.
public class Grid {
// other implementation omitted...
private enum DrawMode {
Background, Walls, Path
}
protected virtual void DrawPath(Cell cell, Graphics g, int cellSize) {
}
public Image ToImg(int cellSize = 50) {
var width = cellSize * Columns;
var height = cellSize * Rows;
var img = new Bitmap(width, height);
using (var g = Graphics.FromImage(img)) {
g.Clear(Color.White);
foreach (var mode in new[]{DrawMode.Background, DrawMode.Walls, DrawMode.Path, }) {
foreach (var cell in Cells) {
var x1 = cell.Column * cellSize;
var y1 = cell.Row * cellSize;
var x2 = (cell.Column + 1) * cellSize;
var y2 = (cell.Row + 1) * cellSize;
if (mode == DrawMode.Background) {
var color = BackgroundColorFor(cell);
if (color != null) {
g.FillRectangle(new SolidBrush(color.GetValueOrDefault()), x1, y1, cellSize, cellSize );
}
} else if (mode == DrawMode.Walls) {
if (cell.North == null) {
g.DrawLine(Pens.Black, x1, y1, x2, y1);
}
if (cell.West == null) {
g.DrawLine(Pens.Black, x1, y1, x1, y2);
}
if (!cell.IsLinked(cell.East)) {
g.DrawLine(Pens.Black, x2, y1, x2, y2);
}
if (!cell.IsLinked(cell.South)) {
g.DrawLine(Pens.Black, x1, y2, x2, y2);
}
} else if (mode == DrawMode.Path) {
DrawPath(cell, g, cellSize);
}
}
}
}
return img;
}
We'll then create a subclass that will implement this DrawPath() method, the ColoredPathGrid. We're actually going to subclass the ColoredGrid class, so that we get all of our nifty colorizing functionality to boot. This isn't as efficient as it could be, and later on we'll be reworking this pretty extensively when we get to non-rectangular grid cells, but for now it works well enough. This will draw a line connecting the cells along the path, with the start and end of the path marked with a square and an X.
public class ColoredPathGrid : ColoredGrid{
public ColoredPathGrid(int rows, int cols) : base(rows, cols) { }
private Distances _path;
private Cell _end;
private int _maxDistance;
public Distances Path {
get => _path;
set {
_path = value;
(_end, _maxDistance) = value.Max;
}
}
public int PathLength => _maxDistance+1;
protected override void DrawPath(Cell cell, Graphics g, int cellSize) {
if (Path == null) {
return;
}
var thisDistance = Path[cell];
if (thisDistance >= 0) {
var x1 = cell.Column * cellSize;
var y1 = cell.Row * cellSize;
var x2 = (cell.Column + 1) * cellSize;
var y2 = (cell.Row + 1) * cellSize;
var cx = cell.Column * cellSize + cellSize / 2;
var cy = cell.Row * cellSize + cellSize / 2;
using (var pen = new Pen(BackColor.Invert(), 2)) {
if (cell.North != null && (Path[cell.North] == thisDistance + 1 || Path[cell.North] == thisDistance - 1 && thisDistance != 0)) {
g.DrawLine(pen, cx, cy, cx, y1);
}
if (cell.South != null && (Path[cell.South] == thisDistance + 1 || Path[cell.South] == thisDistance - 1 && thisDistance != 0)) {
g.DrawLine(pen, cx, cy, cx, y2);
}
if (cell.East != null && (Path[cell.East] == thisDistance + 1 || Path[cell.East] == thisDistance - 1 && thisDistance != 0)) {
g.DrawLine(pen, cx, cy, x2, cy);
}
if (cell.West != null && (Path[cell.West] == thisDistance + 1 || Path[cell.West] == thisDistance - 1 && thisDistance != 0)) {
g.DrawLine(pen, cx, cy, x1, cy);
}
if (thisDistance == 0) {
g.DrawRectangle(pen, cx-2, cy-2, 4, 4);
}
if (thisDistance == _maxDistance) {
g.DrawLine(pen, cx-4, cy-4, cx+4, cy+4);
g.DrawLine(pen, cx+4, cy-4, cx-4, cy+4);
}
}
}
}
}Using this, we can generate images showing paths between cells, or the longest path in a maze.
Whew, that was a lot of code. If you're still with me, I hope you've enjoyed things so far. If you want to download the full solution from GitHub and run it, there's also a little WinForms application that will let you play around with the different algorithms, stepping through them step-by-step, colorizing mazes, drawing paths, and saving out the generated images - it's kind of fun to play around with and experiment.
Next up
Next time, we'll implement some new maze generation algorithms, based on random walks, which will allow us to create mazes that don't have the kind of consistent biases that our previous Binary Tree and Sidewinder algorithms present. In fact, they will be completely unbiased, which has a whole different set of trade-offs. Stay tuned, hopefully it won't take me another month to get the next post written up.



